Zitierfähige Version
Shortfall-Risiko
Geprüftes Wissen

GEPRÜFTES WISSEN
Über 100 Experten aus Wissenschaft und Praxis.
Mehr als 8.000 Stichwörter kostenlos Online.
Das Original: Gabler Banklexikon
zuletzt besuchte Definitionen...
1. Begriff und Terminologie: in einem sehr weiten Sinne das Risiko eines Shortfall, dass man also einem vorgegebenen (Mindest-)Anspruch nicht gerecht wird. Im Kontext des finanziellen Risikomanagements i.w.S. das Risiko, dass eine vorgegeben Mindestzielgröße, z.B. -rendite (analog bzgl. Erfolg, Cashflow, Endvermögen o.Ä.), nicht erreicht wird. Dieses "Risiko" kann nun unterschiedlich aufgefasst werden (vgl. Lower Partial Moments), etwa i.e.S. als Shortfall-Wahrscheinlichkeit im Sinne der bloßen Wahrscheinlichkeit, dass die vorgegebene Mindestrendite unterschritten wird, egal in welchem Umfang. Wird die Mindestrendite so festgelegt, dass sie gleich der zur Erhaltung einer Institution notwendigen minimalen Periodenrendite ist, so ist das Shortfall-Risiko (i.e.S.) gleich der Ausfallwahrscheinlichkeit dieser Institution selbst; ausgehend von diesem besonders plastischen Fall wird der Begriff des Shortfall-Risiko in der deutschsprachigen Literatur auch häufig mit dem Begriff der Ausfallwahrscheinlichkeit gleichgesetzt. Die Mindestrendite wird auch als Shortfall Threshold Level bezeichnet.
2. Berechnung und Veranschaulichung: Falls die Renditen normalverteilt sind, wird das Shortfall-Risiko (i.e.S.) mit folgender Formel ermittelt:
SR = N { [Ri,min – E(Ri)] / σi },
wobei:
Ri = Periodenrendite der Periode i,
N = Funktionswert der kumulativen standardisierten Normalverteilung (Verteilungsfunktion),
Ri,min = Mindestrendite (Shortfall Threshold Level) der Periode i,
E(Ri) = Erwartungswert der Periodenrendite der Periode i,
σi = Standardabweichung der Periodenrendite der Periode i.
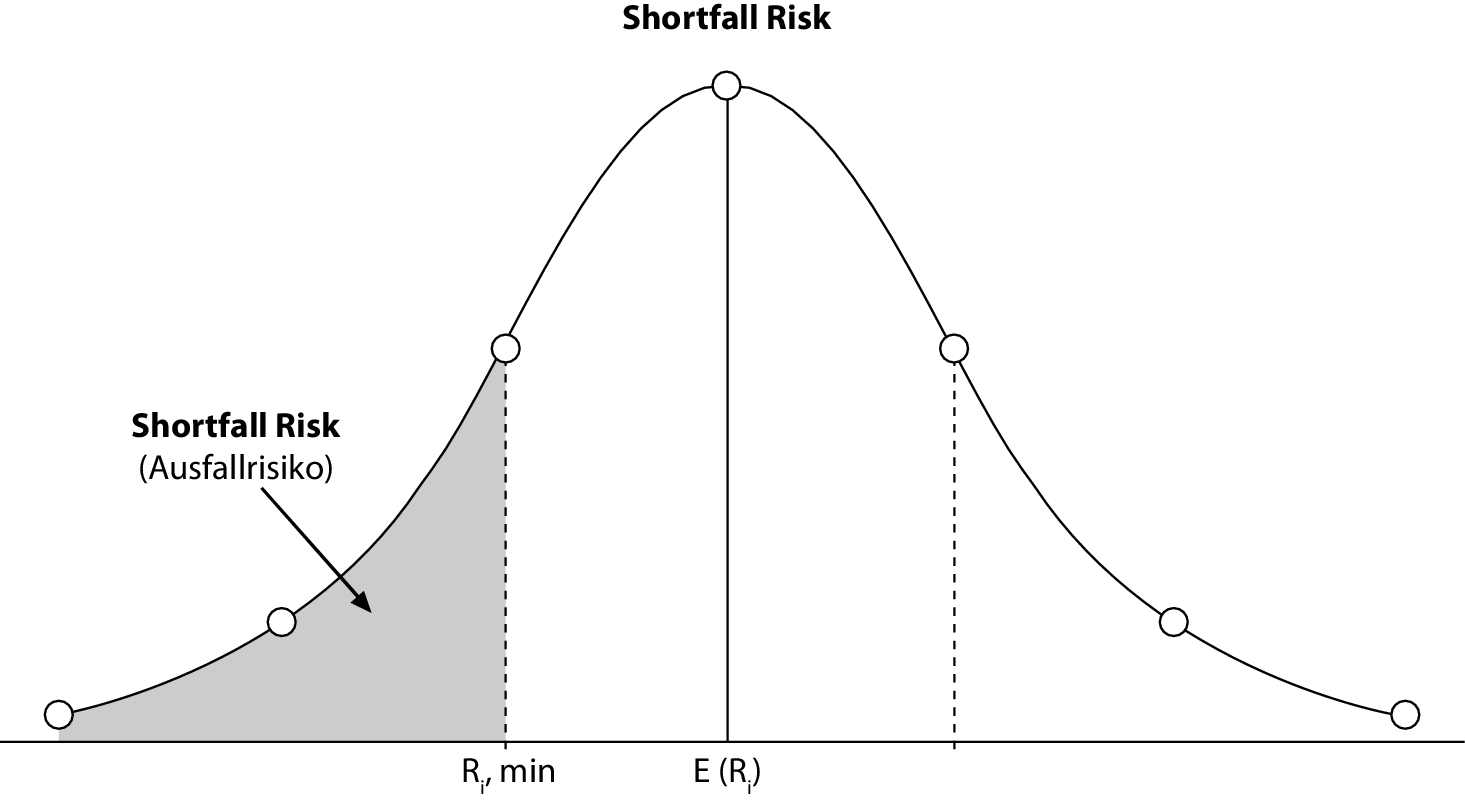
Das Shortfall-Risiko ist hier also von drei Größen abhängig: Je höher die Mindestrendite und je niedriger der Erwartungswert der Periodenrendite ist, desto höher ist die Wahrscheinlichkeit, die Mindestrendite zu unterschreiten; weiterhin steigt das Shortfall-Risiko mit einer höheren Standardabweichung der Periodenrendite. Die Abbildung zeigt, dass das Shortfall-Risiko als Fläche unter der Dichtefunktion der standardisierten Normalverteilung interpretiert werden kann, die links neben der Mindestrendite liegt.
3. Unabhängig von dieser Illustration ist festzuhalten, dass das Konzept des Shortfall-Risikos auch unabhängig von der Annahme der Normalverteilung der Renditen sinnvoll angewandt werden kann – im Unterschied zu den gängigen Risikokennzahlen im Kontext des Mean-Variance-Approach – wobei die mathematische Handhabung anspruchsvoller wird.
4. Zusammenhang mit dem Value-at-Risk: Es besteht ein unmittelbarer Zusammenhang zwischen beiden Größen: Indem der Value at Risk den erwarteten Maximalverlust beschreibt, der nur mit einer bestimmten Wahrscheinlichkeit überschritten wird, ist hierbei eine maximal akzeptierte Shortfall-Wahrscheinlichkeit vorgegeben und wird die dazugehörige Ertragsgröße gesucht; beim Konzept des Shortfall-Risikos ist – genau umgekehrt – eine Mindestertragsgröße vorgegeben und wird die dazugehörige Shortfall-Wahrscheinlichkeit gesucht. Dieser elementare Zusammenhang wird indes dadurch verdunkelt, dass in der Konzeption des Value at Risk erstens dem Planungshorizont deutlich mehr Gewicht eingeräumt wird (als es für oftmals "zeitlose" LPM-Betrachtungen notwendig ist) und zweitens eine Erfolgsgröße in Währungseinheiten untersucht wird (während LPM-Betrachtungen üblicherweise in der Renditedimension erfolgen). Im Kern sind die beiden Konzepte identisch, und der Weg über den Shortfall-Risiko-Ansatz – mit einem wohlbegründeten Shortfall Threshhold Level – kann auch für die Zwecke der Risikosteuerung einer Institution der (jenseits aufsichtlicher Vorgaben) eher arbiträren Setzung eines Konfidenzniveaus für eine VaR-Berechnung überlegen sein.

GEPRÜFTES WISSEN
Über 100 Experten aus Wissenschaft und Praxis.
Mehr als 8.000 Stichwörter kostenlos Online.
Das Original: Gabler Banklexikon