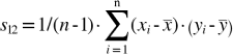Kovarianz

1. Begriff und Einordnung: statistische Maßgröße zur Quantifizierung der Korrelation zweier Zufallsvariablen bzw. quantitativer Merkmale (Zusammenhangs-/Korrelationsmaß). Hiermit können ausschließlich monotone, im Idealfall lineare Zusammenhänge erfasst werden. In der modernen Portfolio-Theorie wird damit die Art des Zusammenhangs, nämlich eine gleichläufige (positive Korrelation) oder aber gegenläufige (negative Korrelation) Entwicklung der Rendite zweier Anlagen/Wertpapiere beschrieben.

2. Berechnung: durchschnittliches Produkt aller Abweichungen zweier Zufallsvariablen von ihrem jeweiligen Erwartungswert (theoretische Kovarianz σ₁₂) bzw. der beobachteten Wertepaare zweier Merkmale in einer Stichprobe von ihrem jeweiligen Mittelwert (empirische Kovarianz). Sind (x_i, y_i) mit i = 1, ... ,n die n beobachteten Wertepaare zweier Merkmale, so ergibt sich speziell deren (erwartungstreue) Stichprobenkovarianz s₁₂ aus der Schätzfunktion

Bild in Originalgröße zeigen

wobei  und  die beiden arithmetischen Mittel sind. Vgl. zum Divisor (n–1) die Ausführungen zur Varianz. Die Varianz selbst stellt sich vor diesem Hintergrund als spezielle Kovarianz mit x = y dar, d.h. die Varianz ist die Kovarianz einer Zufallsvariablen mit sich selbst, während umgekehrt die Kovarianz als Verallgemeinerung der Varianz verstanden werden kann.

3. Interpretation: Eine hohe positive Kovarianz zeigt an, dass die Variable y tendenziell dann eine hohe Ausprägung annimmt, wenn dies auch für die Variable x zutrifft und umgekehrt. Bei der Kovarianz handelt es sich allerdings um ein nichtnormiertes Zusammenhangsmaß – der Wertebereich ist nach oben und unten unbegrenzt –, so dass über die Stärke des Zusammenhangs keine Aussage getroffen werden kann; hierfür bedarf es einer Normierung, wie sie insbesondere bei der Berechnung des Korrelationskoeffizienten durch Standardisierung vorgenommen wird. Weiterhin gilt: Gibt es keinen Zusammenhang zwischen zwei Zufallsvariablen, sind diese also stochastisch unabhängig voneinander, beträgt die Kovarianz Null; der Umkehrschluss ist allerdings nicht zulässig, weil Abhängigkeiten bestehen können, die die Kovarianz rechnerisch nicht erfassen kann.