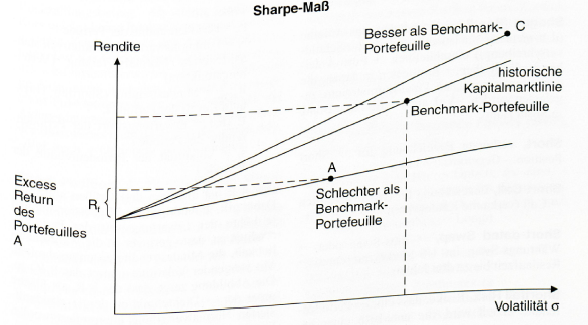
Sharpe-Maß
Übersicht
zuletzt besuchte Definitionen...
Reward-to-Variability-Ratio; Sharpe Ratio; Performance-Kennzahl zur Beurteilung der Performance eines Portfolios. Das Sharpe-Maß setzt die erzielte Überschussrendite ins Verhältnis zur Volatilität der erwirtschafteten Portefeuille-Rendite. Als Überschussrendite oder Excess Return wird die Differenz zwischen der erwirtschafteten Portefeuille-Rendite und dem risikolosen Zinssatz verstanden.
Sharpe-Maß = (rP- rf) / σP
wobei:
rP = gemessene Portefeuille-Rendite
rf = risikoloser Zinssatz
σP = Volatilität der Portefeuille-Rendite im Sinne einer annualisierten Stichproben-Standardabweichung.
Das Sharpe-Maß ist als relative Performance-Kennzahl konzipiert, da sie die Überschussrendite eines Portefeuilles durch Quotientenbildung ins Verhältnis zum Risiko setzt, das durch die Volatilität bzw. Standardabweichung gemessen wird. Hiermit wird also auf das Gesamtrisiko eines Portefeuilles abgestellt. Je höher das Sharpe-Maß, desto besser insoweit die Performance des Portefeuilles bzw. Portfoliomanagers angesehen werden, da eine höhere Risikoprämie je Einheit an übernommenem Gesamtrisiko realisiert werden konnte. Das Sharpe-Maß wird zusätzlich für das Benchmark-Portfolio ermittelt. Liegt das Sharpe-Maß eines Portefeuilles über dem Sharpe-Maß des Benchmark-Portefeuilles, dann ist es dem Portfoliomanagement gelungen, eine höhere risikoadjustierte Rendite zu erzielen, als es bei einer Investition in die Benchmark der Fall gewesen wäre, und umgekehrt.
Das Sharpe-Maß entspricht der Steigung der Geraden in der Abbildung „Sharpe-Maß”. Je steiler die Linie, desto besser war die Performance des Portefeuilles in der Vergangenheit. Die Linie, die den risikolosen Zinssatz mit der Rendite des Benchmark-Portefeuilles verbindet, wird bisweilen als "historische Kapitalmarktlinie" bezeichnet, die nicht auf das Marktportefeuille, sondern auf das Benchmark-Portefeuille bezogen ist. Portefeuilles (z.B. C), die oberhalb dieser Kapitalmarktlinie liegen, weisen eine höhere risikoadjustierte Performance als das Benchmark-Portefeuille auf, d.h. der Portfoliomanager hat die Benchmark risikoadjustiert übertroffen. Portefeuilles (z.B. A), die unterhalb der Kapitalmarktlinie liegen, weisen eine geringere risikoadjustierte Performance als das Benchmark-Portefeuille auf.
Kritisch ist zunächst festzuhalten, dass die Tendenz besteht, durch Orientierung am Sharpe-Maß risikoärmere Portefeuilles zu bevorzugen: Im Vergleich zur Benchmark risikoreichere Portefeuilles mögen zwar ein niedrigeres Sharpe-Maß aufweisen, aber um ein vom Gesamtrisiko her vergleichbares Portefeuille über eine Investition in die Benchmark herzustellen, müsste diese z.T. kreditfinanziert werden, und zwar annahmegemäß zum gleichen Zinssatz wie dem der risikolosen Anlage; dies ist in der Quotientenbildung impliziert und dürfte in den meisten Situationen unrealistisch sein (vgl. auch Portfolio-Theorie, Modellkritik, Ziff. 2.)). Des Weiteren wird mit der Bezugnahme auf das Gesamtrisiko des Portefeuilles nicht zwischen dessen Bestandteilen, dem systematischen und dem unsystematischen Risiko, unterschieden. Sachgerecht ist dies nur dann, wenn es sich bei dem betrachteten Portefeuille um das Gesamtportefeuille des Anlegers handelt, da nur in diesem Fall das Gesamtrisiko ausschlaggebend ist. Ist das zu bewertende Portefeuille hingegen nur ein Teilportefeuille innerhalb eines gut diversifizierten Gesamtportefeuilles, ist zur Beurteilung der Performance dieses Portefeuilles nur das systematische Risiko relevant, weil sich die unsystematische Risikokomponente durch Diversifikation innerhalb des Gesamtportefeuilles weitgehend eliminieren lässt. Dies berücksichtigt das Treynor-Maß, in dem – ansonsten in der Struktur dem Sharpe-Maß entsprechend – anstelle der Relativierung der erzielten Überschussrendite durch das eingegangene Gesamtrisiko auf das Beta-Risiko Bezug genommen wird. Hierfür muss ein hinreichender Diversifikationsgrad des Gesamtportefeuilles gegeben sein, wohingegen der Aspekt der Diversifiziertheit beim Sharpe-Maß für dessen Aussagekraft keine Rolle spielt. Weil diese Bedingung nicht unbedingt erfüllt sein muss, wird häufig empfohlen, Sharpe-Maß und Treynor-Maß komplementär zu verwenden, um eine bessere Beurteilungsgrundlage zu gewinnen.
Vgl. auch Portfolio-Theorie, Performance-Messung.
Literaturhinweise SpringerProfessional.de
Bücher auf springer.com
Interne Verweise
Sharpe-Maß
Sharpe-Maß
- Benchmark-Portfolio
- Beta-Risiko
- Diversifikation
- Excess Return
- Gesamtrisiko
- Marktportefeuille
- Performance
- Performance-Messung
- Portefeuille-Rendite
- Portfolio
- Portfolio-Theorie
- Portfolio-Theorie, Weiterentwicklungen
- Standardabweichung
- systematisches Risiko
- Treynor-Maß
- unsystematisches Risiko
- Volatilität