Zitierfähige Version
Markt-Modell
Geprüftes Wissen

GEPRÜFTES WISSEN
Über 100 Experten aus Wissenschaft und Praxis.
Mehr als 8.000 Stichwörter kostenlos Online.
Das Original: Gabler Banklexikon
zuletzt besuchte Definitionen...
1. Einordnung: Empirisch ausgerichtetes Faktormodell zur Modellierung des renditegenerierenden Prozesses (und darauf aufbauend zur Schätzung) von Wertpapier-, insbesondere Aktienrenditen auf der Grundlage eines einzigen (Einfluss-)Faktors, der Marktentwicklung. Innerhalb der Faktormodelle kommt dem Markt-Modell eine gewisse Sonderstellung zu, weil die Bedeutung der Entwicklung "des Marktes" durch das Capital Asset Pricing Model (CAPM) gleichgewichtstheoretisch fundiert werden konnte. Dieses Fundament beinhaltet allerdings wesentlich die Einbeziehung einer risikolosen Anlagemöglichkeit, so dass im CAPM die Erklärung der Überschussrendite (Rendite abzüglich dem risikolosen Zinssatz) als Risikoprämie zentraler Gegenstand der Betrachtungen ist. Demgegenüber wird in der ursprünglichen Version des Markt-Modells die Entwicklung der gesamten Wertpapierrendite auf die Entwicklung des Marktes zurückgeführt; die Existenz eines risikolosen Zinssatzes muss hier nicht unterstellt werden. Da weder der allgemeine Marktfaktor noch das sog. Marktportefeuille (des CAPM) unmittelbar beobachtet werden können, wird als Stellvertreter auf einen für hinreichend repräsentativ gehaltenen Aktienindex zurückgegriffen. Damit konnte für das Markt-Modell unmittelbar an das zuvor – zu ganz anderen, portfoliotheoretischen Zwecken – entwickelte Index-Modell von Sharpe angeknüpft werden. Wenn also der empirische Charakter des Markt-Modells in den Vordergrund gestellt wird, ist auch vom ökonomischen Sprachgebrauch her (vgl. ansonsten Multi-Index-Modelle, Ziff. 2)) nachvollziehbar, dass von einigen Autoren anstelle des Begriffes "Markt-Modell" die Bezeichnung "Single-Index-Modell" bevorzugt wird.
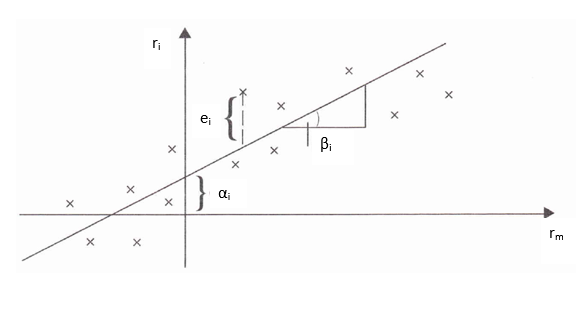
2. Modellstruktur: Beim Markt-Modell wird ein linearer Zusammenhang zwischen der Marktrendite und der Rendite eines Wertpapiers postuliert – und nicht wie im CAPM als Modellergebnis (und Hypothese) geschlussfolgert. Dies geschieht, um eine lineare Einfachregression (Regressionsanalyse) durchführen zu können, die in der ursprünglichen Version des Markt-Modells auf folgender Regressionsfunktion basiert:
ri = αi + βirm + ui
wobei:
ri = Rendite des i-ten Wertpapiers,
αi = von der Marktrendite unabhängige Wertpapierrendite (Alpha-Faktor im Sinne des Markt-Modells),
βi = Beta-Faktor des i-ten Wertpapiers,
rm = Rendite des Gesamtmarktes (bzw. Marktindex),
ui = Residualrendite als (empirischer) Zufallsfehler.
Ergebnis dieser Regression ist eine Regressionsgerade, die wertpapierspezifische sog. Security Characteristic Line (SCL), die innerhalb einer Punktewolke der gemessenen historischen Werte für ri und rm die Summe der (quadratischen) vertikalen Abweichungen der Renditepaare von dieser Linie minimiert. Dies zeigt die Abbildung "Die Wertpapierrendite in Abhängigkeit von der Marktrendite".
In der moderneren Überschussrendite-Version erfolgt statt dessen die Regression der Überschussrendite des Wertpapiers ri–rf auf die Überschussrendite des Marktes rm–rf, wobei rf den (existierenden) risikolosen Zinssatz bezeichnet; damit wird das Markt-Modell stärker an das CAPM herangerückt und insoweit schärfer plausibilisiert. In beiden Versionen wird unterstellt, dass der durch die Regression gemessene Zusammenhang über den gesamten Beobachtungszeitraum konstant ist. So wird jedes Wertpapier durch seine individuellen Alpha- und Beta-Werte charakterisiert. Inhaltlich lässt sich dies so interpretieren, dass die Rendite eines Wertpapiers in zwei Komponenten zerlegt werden kann: einerseits die systematische (marktbezogene) Rendite, die durch den Beta-Faktor bestimmt ist und die auf alle Wertpapiere eines Marktes wirksame Einflussfaktoren (z.B. Zinsänderungen, Rohstoffpreisentwicklungen, wie Ölpreisschocks, oder Wahlausgänge) repräsentiert, und andererseits die unsystematische (wertpapierbezogene) Rendite, die der Alpha-Faktor abbildet und die (im Aktienbereich) unternehmensspezifische Einflüsse (z.B. bedeutsame Innovationen, Vorstandswechsel) einfängt. Gleiches gilt hinsichtlich der Zerlegung des Gesamtrisikos einer Wertpapieranlage; vgl. hierzu ausführlich systematisches Risiko und unsystematisches Risiko (sowie Residualvarianz, - volatilität). Speziell letzteres wird im sog. (empirischen) Zufallsfehler ui (Residualrendite) sichtbar, für den ein Erwartungswert von null, eine konstante Varianz und eine Korrelation (Korrelationskoeffizient) von null mit der Marktrendite angenommen wird; vgl. hierzu kritisch Index-Modell. Das sog. Bestimmtheitsmaß (Determinationskoeffizient) R2 gibt an, wieviel Prozent der Varianz einer Wertpapierrendite durch die vorgenommene Regression erklärt werden können und quantifiziert damit die Aussagekraft der Regression; speziell im Markt-Modell lässt es sich als Quotient aus der Varianz der Marktrendite (σm2) und der Varianz der Wertpapierrendite (σi2), multipliziert mit dem quadrierten Betafaktor berechnen: R2 = βi2 · (σm2/σi2).
3. Anwendung: Die ursprüngliche Anwendungsidee des Markt-Modells bestand darin, unter der Annahme gleichbleibend hoher Alpha- und Beta-Faktoren aus der Prognose der Renditeentwicklung des Gesamtmarktes zu einer Renditeschätzung für ein einzelnes Wertpapier vorzudringen; dies hat sich allerdings vor allem mangels im Zeitablauf stabiler Alpha-Faktoren als nicht tragfähig erwiesen (vgl. hierzu Alpha-Faktor). Ein solcher Ansatz kommt bestenfalls für die Renditeschätzung größerer Portefeuilles infrage, bei denen auf einen Fehlerausgleich bei den Schätzparametern gehofft werden kann (vgl. Portefeuille-Alpha). Im Unterschied hierzu ist die Risikoschätzung und damit die historisch basierte Schätzung der Beta-Faktoren auch einzelner Wertpapiere aus der ermittelten Regressionsgleichung heraus in der Praxis weiterhin weit verbreitet, da eine als hinreichend erachtete Stabilität der Beta-Faktoren im Zeitablauf beobachtbar ist und zudem die dahingehenden Schätzungen durch spezielle statistische Verfahren (Adjusted Beta) verfeinert werden konnten. Wird vor diesem Hintergrund die Schätzung einer Wertpapierrendite anderweitig vorgenommen, z.B. im Aktienbereich nach gängigen Dividendenbewertungsmodellen, und diese mit einem geschätzten Beta-Faktor zusammengeführt, lässt sich aus dem Markt-Modell in der Überschussrendite-Version eine implizite Überschussrendite des Marktes und damit letztlich eine Vorstellung von der aktuellen Risikoübernahmebereitschaft (Risikoappetit) am Kapitalmarkt, gemessen am sog. "Marktpreis des Risikos" (nach dem CAPM, dort Ziff. 2) gewinnen – und in timingorientierten Anlagestrategien umsetzen.
Vgl. auch Risikoarten von Wertpapieren, Portfolio-Theorie, statistische Methoden, Faktormodelle, Asset Allocation.

GEPRÜFTES WISSEN
Über 100 Experten aus Wissenschaft und Praxis.
Mehr als 8.000 Stichwörter kostenlos Online.
Das Original: Gabler Banklexikon