Capital Asset Pricing Model (CAPM)

1. Einordnung: Das CAPM ist das Herzstück der modernen Kapitalmarkttheorie. Das Grundmodell wurde Mitte der 1960er-Jahre in verschiedenen Beiträgen von Sharpe, Lintner und Mossin unabhängig voneinander entwickelt. Ziel ist die Herleitung gleichgewichtiger und insoweit zu erwartender Renditen in Abhängigkeit vom Risiko in einem zu beschreibenden Kapitalmarktgleichgewicht, und zwar sowohl für effiziente Portefeuilles als auch für einzelne Wertpapiere. Neben den üblichen Annahmen über einen vollkommenen Kapitalmarkt baut das CAPM wesentlich auf der Portfolio-Theorie von Markowitz auf, indem davon ausgegangen wird, dass sich die annahmegemäß rationalen und risikoscheuen Anleger genauso verhalten, wie es ihnen von der Portfolio-Theorie empfohlen wird. Von daher treffen die Anleger ihre Anlageentscheidungen in Abhängigkeit vom Erwartungswert der Portefeuille-Rendite und deren Varianz bis zum Ende eines einperiodigen Anlagehorizonts (Mean-Variance-Approach). Das CAPM i.w.S. besteht aus zwei Teilen: dem Modell der Kapitalmarktlinie und dem eigentlichen CAPM, dem Modell der Wertpapierlinie.

2. Modell der Kapitalmarktlinie: Die Kapitalmarktlinie ergibt sich in der Grundversion des CAPM aus dem Zusammenwirken dreier – nicht unproblematischer – Annahmen: Erstens wird unterstellt, dass alle Anleger zu einem risikolosen Zinssatz beliebig hohe Beträge sowohl anlegen als auch im Wege eines Kredites aufnehmen können. Im Ergebnis sieht sich jeder Anleger einer (individuellen) neuen, linear verlaufenden Effizienzkurve gegenüber, auf der er in Abhängigkeit von seiner Risikoeinstellung sein optimales Portefeuille ausschließlich aus der "risikolosen Anlage" (bzw. einer Verschuldung zu gleichen Konditionen) und einem Teilportefeuille aus risikobehafteten Anlagen zusammenstellt (Two-Fund-Theorem); dieses Teilportefeuille aus ausschließlich risikobehafteten Anlagen ist durch den Tangentialpunkt mit der ursprünglichen Effizienzkurve als sog. Tangentialportefeuille eindeutig identifizierbar; vgl. Portfolio Selection. Die zweite Annahme besteht darin, dass die Anleger identische (homogene) Erwartungen über die Erwartungswerte, Varianzen und Kovarianzen der Wertpapierrenditen hegen, so dass die ursprünglichen Effizienzkurven aller Anleger identisch sind. Wenn zusätzlich davon ausgegangen wird, dass der risikolose Zinssatz für alle Anleger gleich hoch ist, ermitteln alle Anleger dasselbe Tangentialportefeuille (Tobinsches Separationstheorem); alle Anleger fragen also dasselbe Teilportefeuille aus risikobehafteten Anlagen nach. Zum dritten wird schließlich angenommen, dass ein Marktgleichgewicht herrscht, in dem diese Nachfrage nach risikobehafteten Anlagen mit dem Angebot übereinstimmt. Außerhalb dieses Gleichgewichts setzen annahmegemäß Marktprozesse und damit Kursbewegungen ein, durch die bspw. der Kurs eines Wertpapiers mit einem ungleichgewichtig hohen Kurs solange sinkt, bis auch dieses von den Anlegern in das nachgefragte Teilportefeuille risikobehafteter Anlagen aufgenommen wird. In diesem müssen sämtliche risikobehaftete Anlagen enthalten sein, weil sie wegen der annahmegemäß homogenen Erwartungen der Marktteilnehmer sonst von niemandem gehalten werden. Damit muss es sich bei dem Tangentialportefeuille um das sog. Marktportefeuille handeln, in dem alle risikobehafteten Anlagen im Verhältnis ihres Marktwertes zum Gesamtmarktwert des Marktportefeuilles enthalten sind.

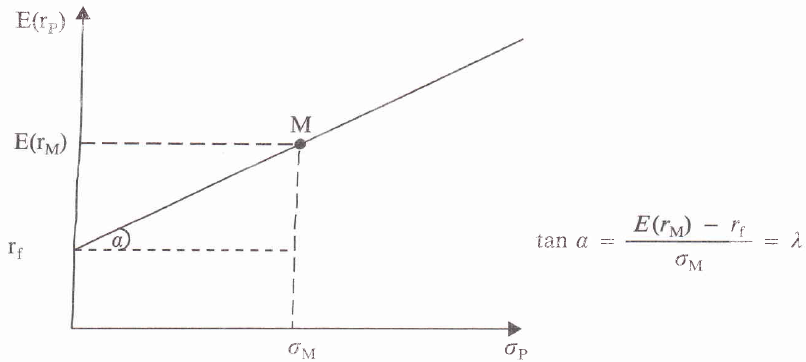
Die Kapitalmarktlinie (Capital Markt Line, CML) als Linie effizienter Portfeuilles im Marktgleichgewicht verläuft also ausgehend vom risikolosen Zinssatz r_f linear zu dem Punkt M, der die zu erwartende Rendite des Marktportefeuilles E(r_M) und dessen Risiko, gemessen an der Standardabweichung σ_M, kennzeichnet, und (für den Verschuldungsfall) darüber hinaus; dies zeigt die Abbildung "Der Marktpreis des Risikos auf der Kapitalmarktlinie". Ihre Steigung (λ) ergibt sich aus den Werten für E(r_M) und σ_M; weil sie durch die skizzierten Marktprozesse eindeutig determiniert ist, wird diese Größe auch als "Marktpreis des Risikos" bezeichnet. Er gibt darüber Aufschluss, wieviel zusätzliche Renditeeinheiten ein Anleger erwarten kann, der bereit ist, eine weitere Einheit Risiko auf sich zu nehmen, also von der risikolosen Anlage aus stärker in das Marktportefeuille zu investieren (oder sogar kreditfinanziert darüber hinaus). Im Ergebnis zeigt die Gleichung der Kapitalmarktlinie die gleichgewichtige und insoweit zu erwartende Rendite eines effizienten Portefeuilles E(r_P) an:

Sie setzt sich also aus dem risikolosen Zinssatz und einer Risikoprämie zusammen, die sich aus der je nach Risikoeinstellung konkret übernommenen "Risikomenge" σ_P und dem dafür erzielten "Preis" ergibt.

Bild in Originalgröße zeigen

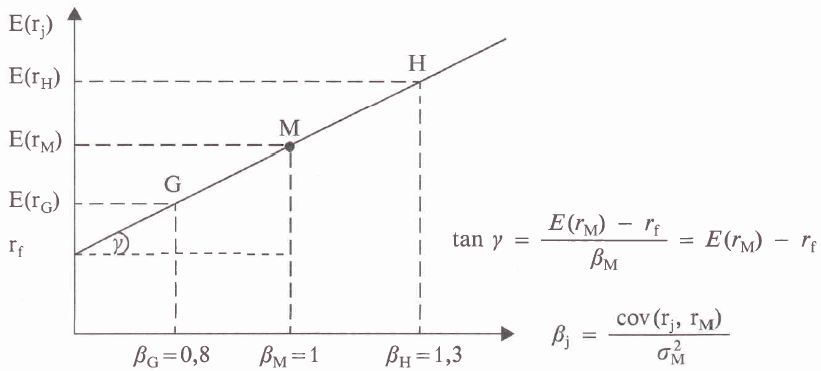
3. Modell der Wertpapierlinie: Das CAPM i.e.S. widmet sich ausgehend hiervon der Frage, welche Rendite sich für ein einzelnes Wertpapier im Kapitalmarktgleichgewicht einstellt, wenn dieses nicht isoliert, sondern innerhalb eines effizienten Portefeuilles gehalten wird. Aus dem Vorangehenden folgt, dass es sich hierbei um den spezifischen Beitrag des Wertpapiers zum Risiko des Marktportefeuilles handeln muss. Wenn dieses Portefeuille-Risiko durch die Varianz gemessen wird, kann der Risikobeitrag – wie bei jedem anderen Portefeuille (Portefeuille-Varianz) – in der durchschnittlichen Kovarianz der Rendite des Wertpapiers j mit der aller anderen Anlagen im Marktportefeuille (einschließlich der des Wertpapiers selbst: Varianz als spezielle Kovarianz) und damit in der Kovarianz der Rendite des Wertpapiers mit der Rendite des Marktportefeuilles cov (r_j, r_M) gesehen werden. Diese absolute "Risikomenge" lässt sich dann auf die "Risikomenge" des Marktportefeuilles σ_M² beziehen, deren "Gesamtpreis" bereits im Modell der Kapitalmarktlinie als E(r_M) – r_f abgeleitet worden war; dieser relative Risikobeitrag eines Wertpapiers zum Marktportefeuille wird als Beta-Risiko bezeichnet. Somit ergibt sich die Gleichung der Wertpapierlinie (Security Market Line, SML) für die gleichgewichtige und insoweit zu erwartende Rendite eines Wertpapiers in Abhängigkeit von der spezifischen Risikohöhe des Wertpapiers innerhalb des Marktportefeuilles:

Anstelle dieser intuitiven Überlegungen wird dies in der Literatur auch auf haushaltstheoretischer Grundlage exakt abgeleitet. Die Struktur der Wertpapierlinie ist ähnlich wie die der Kapitalmarktlinie – mit dem entscheidenden Unterschied, dass sich das Risiko und die dazugehörige Risikoprämie eines einzelnen Wertpapiers im Unterschied zum Risiko eines effizienten Portefeuilles als ganzem nur nach dem Risikobeitrag zu einem solchen effizienten Portefeuille und damit dem Marktportefeuille bemisst; dieser wird durch den Beta-Faktor β_j bestimmt. Die Abbildung "Wertpapierpreise auf der Security Market Line" zeigt den Verlauf der Wertpapierlinie, deren Steigung (γ) sich daraus ergibt, dass das Beta-Risiko des Marktportefeuilles β_M selbst gleich Eins ist. Die zentralen Modellaussagen lauten somit: Erstens besteht ein linearer Zusammenhang zwischen der Rendite eines Wertpapiers und sowohl der Rendite "des Marktes" (während andere Einflussgrößen/Risikofaktoren unbeachtlich seien) als auch des Beta-Risikos bzw. Beta-Faktors des Wertpapiers; für ein insoweit risikoärmeres Wertpapier mit einem Beta-Faktor β_G ist eine niedrigere Rendite E(r_G) zu erwarten als für ein insoweit risikoreicheres Wertpapier mit einem Beta-Faktor von β_H und einer Rendite von E(r_H). Zweitens sollte im Kapitalmarktgleichgewicht nicht das absolute, also das Gesamtrisiko eines Wertpapiers, sondern nur das Beta-Risiko als sog. systematisches Risiko bewertungsrelevant sein, also dessen Übernahme in Form einer Risikoprämie entgolten werden; die verbleibende Komponente des unsystematischen Risikos ist durch Diversifikation weitgehend, und theoretisch innerhalb des Marktportefeuilles sogar vollständig, eliminiert.

Bild in Originalgröße zeigen

4. Modellerweiterungen: Die wichtigsten Weiterentwicklungen des CAPM sind naturgemäß mit der Aufweichung der rigiden Prämissenlandschaft des CAPM in seiner Grundversion befasst. Es konnte insbesondere gezeigt werden, dass unter bestimmten Bedingungen ein linearer Zusammenhang zwischen der Wertpapierendite und einem Beta-Faktor in modifizierter Form sowohl bei Nichtexistenz einer risikolosen Anlage (sog. Zero-Beta-Modell von Black) als auch bei heterogenen Erwartungen der Marktteilnehmer (Lintner) existiert; die Eigenschaft der Tobin-Separation ist dann allerdings für die Zwecke der praktischen Anwendung nur noch schwer interpretierbar (Black) bzw. unmittelbar nicht mehr gegeben (Lintner). Weitere wichtige Modifikationen gelten u.a. der Einbeziehung von Steuern und Transaktionskosten, nicht handelbarer unsicherer Anlagen (insbesondere Humankapital), einer mehrperiodigen, dynamischen Betrachtungsweise (Three-Fund-Theorem) und der – von der Kritik an der Annahme einer Normalverteilung der Renditen ausgehenden – Berücksichtigung downside orientierter Risikomaße (vgl. dazu Mean-LPM-Approach). Insgesamt ist festzuhalten, dass die Grundstruktur des CAPM gegenüber Veränderungen in der Annahmenliste erstaunlich robust ist und sich insbesondere die Modellaussage eines linearen Zusammenhangs zwischen Rendite und (systematischem) Risiko als sehr belastbar erwiesen hat.

5. Modellkritik: Auch vor diesem Hintergrund entzündet sich die Kritik am CAPM vor allem auf empirischer Ebene, zum einen hinsichtlich der Testergebnisse zu den aus dem CAPM ableitbaren Hypothesen und zum anderen hinsichtlich der Testbarkeit des CAPM schlechthin.

a) Zur Flachheit der Wertpapierlinie: Der empirische Befund zeichnet kein eindeutiges Bild, ist aber summa summarum als leicht positiv, zugunsten des CAPM zu werten, insbesondere für den US-amerikanischen Raum. Dabei ließ sich allerdings feststellen, dass – bei weitgehender Bestätigung der Linearitätshypothese – der Ordinatenabschnitt der ermittelten Wertpapierlinie systematisch höher liegt als es aus dem CAPM heraus zu erwarten gewesen wäre; der Frage "Warum verläuft die Wertpapierlinie so flach?" ist in zahlreichen Studien nachgegangen worden. Interessant ist etwa, dass der marktimplizierte Shortfall Threshold Level lt. Mean-LPM-Approach eher im Bereich der erwarteten Portefeuille-Rendite und damit deutlich höher liegt als der CAPM-implizierte Shortfall Threshold Level: Dies ist – stillschweigend angenommen – der risikolose Zinsssatz.

b) Renditeanomalien und konkurrierende Modelle: Des weiteren scheinen weitere bewertungsrelevante Faktoren auf, die aus Sicht des CAPM als "Renditeanomalien" gedeutet und als solche diskutiert werden, Anlass zur Entwicklung dahingehender Mehrfaktorenmodelle (z.B. Dreifaktorenmodell) gegeben und Zweifel an der Grundannahme rationalen Verhaltens der Marktteilnehmer aufgeworfen haben, z.B. bei saisonalen Effekten wie dem Januareffekt oder dem Wochenendeffekt. Die Mehrfaktorenmodelle werden theoretisch abgestützt durch die Arbitrage Pricing Theory (APT), die im Unterschied zum CAPM in ihrer Grundversion nicht mehr gleichgewichts- und damit haushaltstheoretisch fundiert ist und statt dessen auf einem geschlossenen Arbitragesystem basiert. Nachdem APT und Mehrfaktorenmodelle dem CAPM und dem Markt-Modell, nicht zuletzt in der Gunst der Praxis, zeitweise überlegen schienen, mehren sich inzwischen Zweifel an der Relevanz von Mehrfaktorenmodellen und damit der APT in ihrer bisherigen Form durch Studien zu einer sog. konditionierten Anlagebewertung durch die Marktteilnehmer (vgl. dazu Faktormodelle, Ziff. 5). Auch das CAPM bleibt von dahingehend negativer Evidenz nicht verschont, findet beachtlicherweise aber auch indirekte Unterstützung: Zwar erscheint der Erklärungsgehalt des "klassischen" Beta-Faktors und seiner Veränderungen gering zu sein – daher ja auch der zuvor erwähnte flache Verlauf der Wertpapierlinie –, aber von allen in Frage kommenden (Faktor-)Risikoprämien erweist sich gerade der "Marktpreis des Risikos" aus dem CAPM als die Risikoprämie, deren prognostizierbare zeitliche Schwankungen die rational erwartbare Anlagerendite im Zeitablauf am meisten prägt. Kurz gefasst wird die gleichgewichtige Aktienrendite offenbar weniger durch Veränderungen des Beta dieser Aktie als vielmehr durch Veränderungen des Preises für die Übernahme dieses Beta bestimmt; sogar die Korrelation zwischen der Höhe des Beta und der Höhe seines Preises kann eine größere Rolle spielen als die Höhe des Beta allein. Mit anderen Worten dürfte der Fokus, den das CAPM auf die Entwicklung "des Marktes" gelegt hat, der richtige gewesen sein, aber am ehesten deshalb, weil die Entwicklung eines risikobehafteten Marktes auf die Höhe der dort geforderten Risikoprämie zurückwirkt.

c) Zur Testbarkeit des CAPM: Ebenso wichtig, aber schon seit langem bekannt, ist die von Roll (1977) in Zweifel gezogene Testbarkeit des CAPM überhaupt: Zum einen ist das Marktportefeuille als solches nicht erhebbar und wird in empirischen Untersuchungen durch einen für hinreichend repräsentativ gehaltenen Marktindex, insbesondere einen Aktienindex, ersetzt. Zum anderen ist gezeigt worden, dass sich eine lineare Rendite-Risiko-Beziehung auf der Grundlage jedwedes (risiko-)effizienten Portefeuilles ableiten lässt, also eine Tautologie darstellt. Testbar ist demzufolge nur die Risikoeffizienz des herangezogenen Index, jenseits der im CAPM formulierten Marktprozesse, die die Risikoeffizienz des Marktportefeuilles sicherstellen sollen. Diese steht inhaltlich ohnehin in Frage, weil außerhalb des postulierten Gleichgewichtszustandes auch die Risikoeffizienz des Marktportefeuilles selbst nicht gewährleistet ist. Abschließend ist festzuhalten, dass das CAPM trotz dieser Kritikpunkte seinen Stellenwert als Grundpfeiler und Ankerpunkt der gleichgewichtstheoretisch angelegten Kapitalmarkttheorie in Forschung und Praxis erhalten hat.